Ruining Games: Digits

If you’re looking to fill the Wordle shaped hole in your heart, Digits is a fun math game recently released by The New York Times. The rules are simple:

1. You’re given six numbers, and a separate target number.
2. Using only addition, subtraction, multiplication, and division, create an expression that evaluates to the target number.
3. No negative numbers or fractions are allowed, and not all numbers need be used.

If you had fun playing 24 by yourself as a kid, then you’ll love this game. At least, that’s what I thought until they gave me this problem:

I hope that you solve this one quickly and enjoyably - I didn’t. It took 45 minutes, while at work, and I didn’t even succeed. This infuriating encounter reminded me of this quote I first read in Peter Norvig’s Sudoku post:

Sudoku is “a denial of service attack on human intellect”.

Why am I spending time number crunching when my computer can do that for me?? I should write a Digits solver for fun and to convince myself never to spend 45 minutes that way again.

Representation

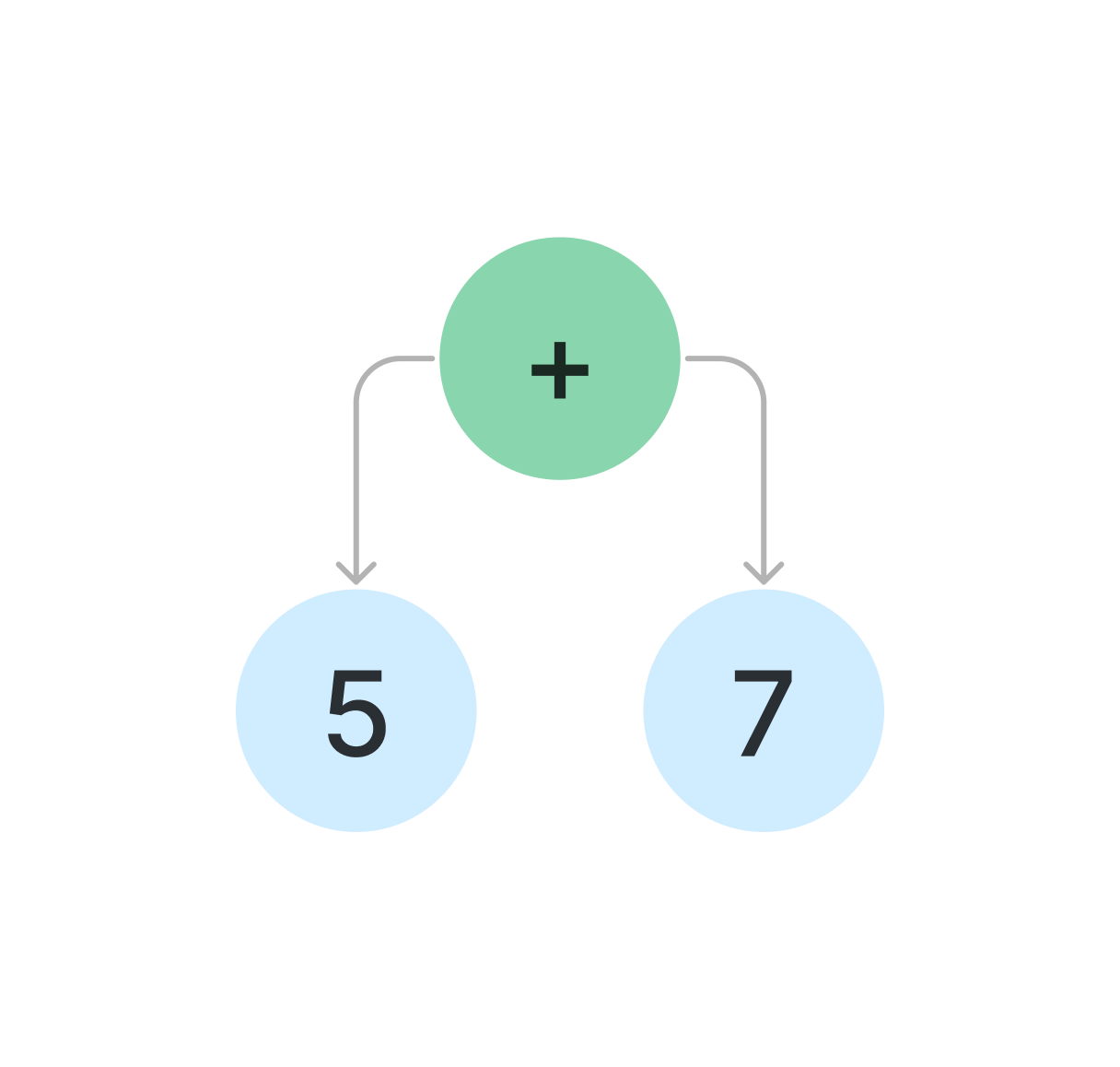
As you play Digits, you sequentially choose numbers and operations, gradually removing numbers hoping to eventually find the target number. But what you’re actually doing is building an arithmetic tree. For example, if you type 5 + 7, that’s equivalent to the tree below:

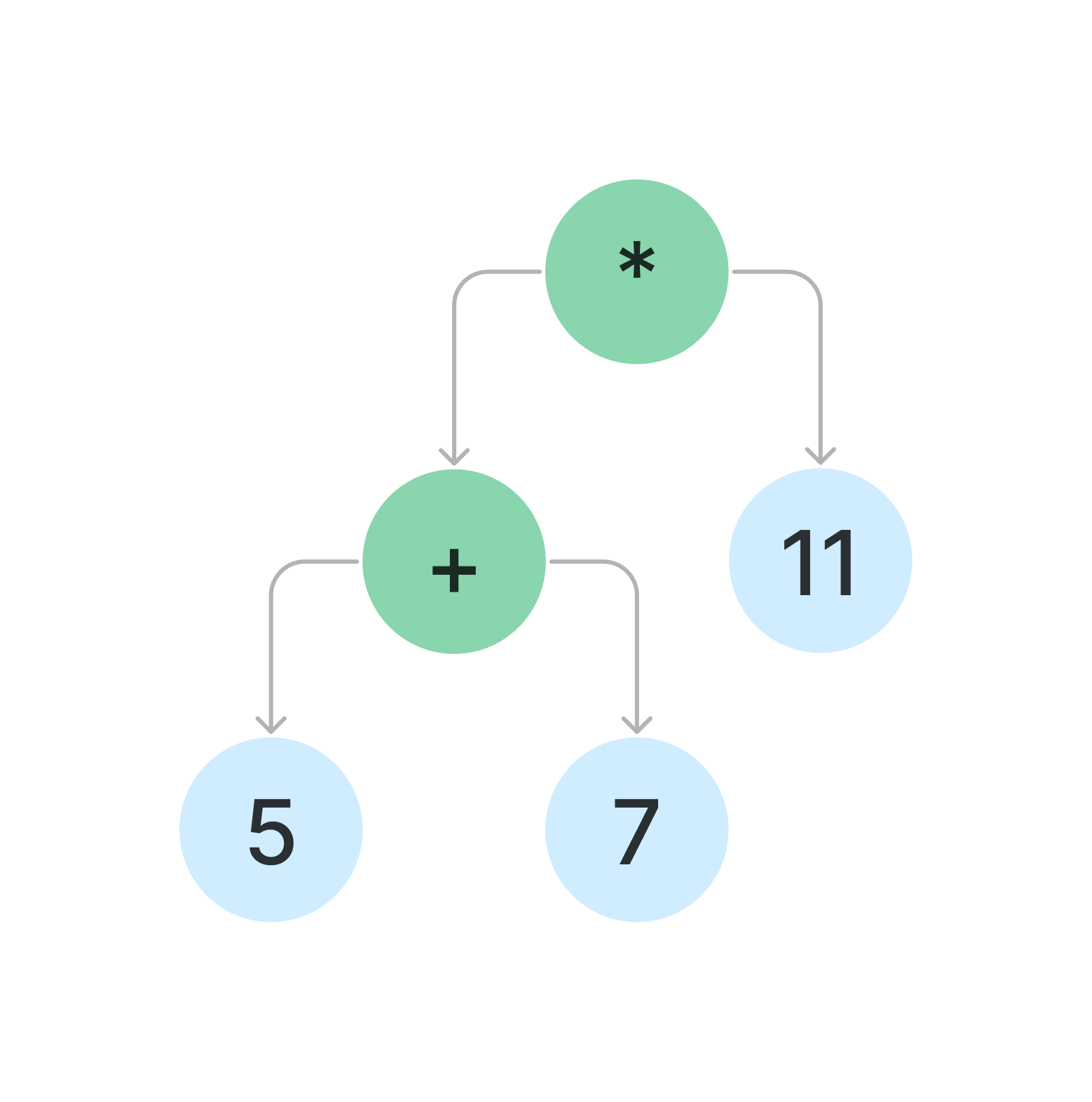
A more complex expression, like (5 + 7) * 11, would be equivalent to a more complex tree:

(Side note: if you’re intrested in how CS concepts like trees can be used to improve math education, check out Bootstrap)

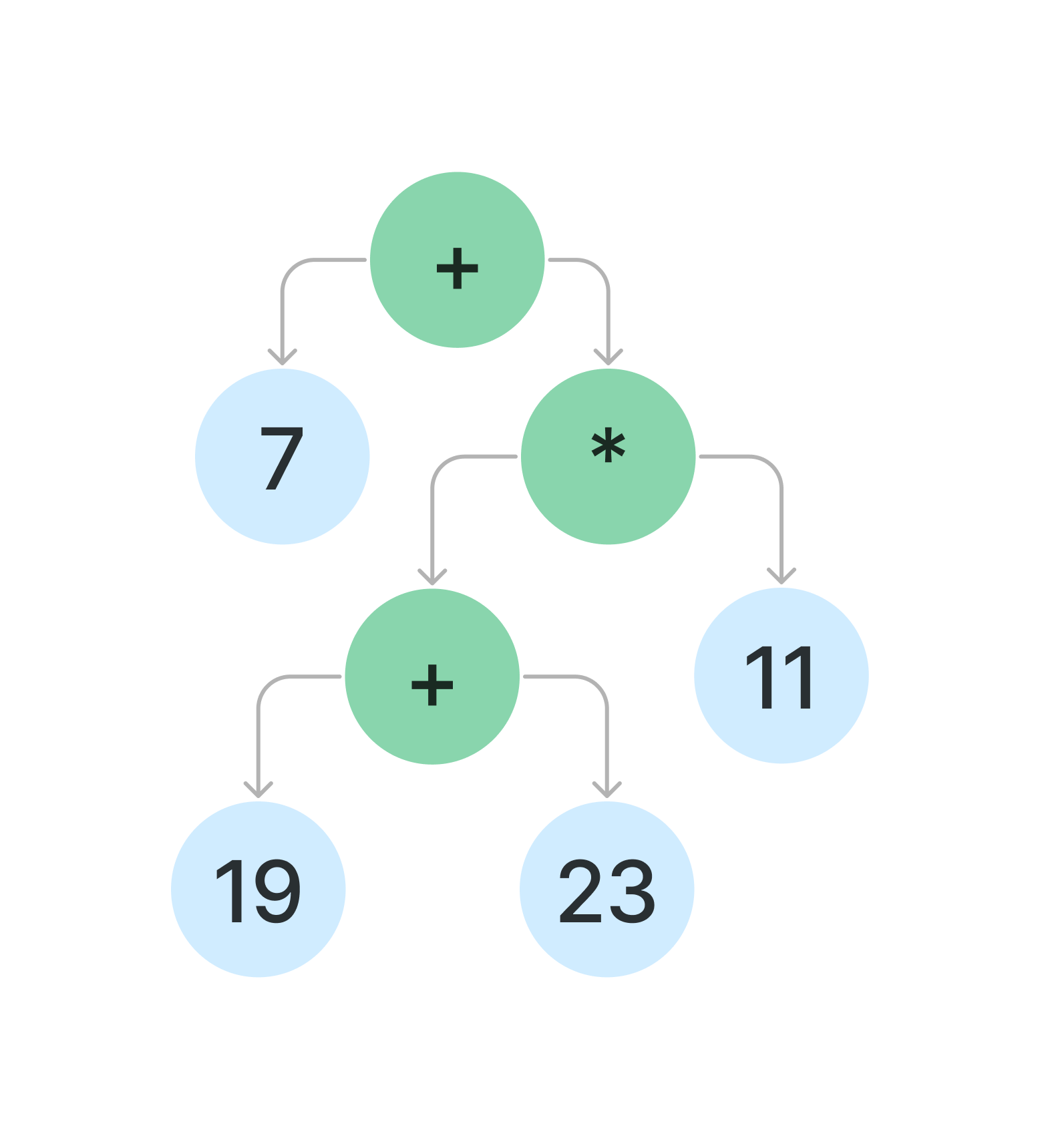
Notice that complex expressions can be made of integer expressions or complex sub-expressions. For the Digits puzzle that drove me crazy, this tree represents one possible solution:

To represent these expressions in Kotlin (my current language of choice), there are two kinds of expressions to consider; regular integers (like 5), or binary expressions (like 5 + 7). Binary expressions are made up of a left hand side, an operator (+, -, *, /) and a right hand side. Binary expressions are more interesting, because the left & right sides can themselves be binary expressions:

enum class Operator {
  PLUS,
  MINUS,
  TIMES,
  DIVIDED_BY;
}

sealed class Expr {

  data class IntExpr(val value: Int) : Expr()

  data class BinaryExpr(
    private val left: Expr, 
    private val operator: Operator,
    private val right: Expr
  ): Expr()
}

Here’s how we would write the three expressions above, in Kotlin:

IntExpr(value = 5)

BinaryExpr(
  left = IntExpr(5),
  right = IntExpr(7),
  operator = Operator.PLUS
)

BinaryExpr(
  left = IntExpr(5),
  right = BinaryExpr(
    left = BinaryExpr(
      left = IntExpr(19),
      right = IntExpr(23),
      operator = Operator.PLUS
    ),
    right = IntExpr(11),
    operator = Operator.TIMES
  ),
  operator = Operator.PLUS
)

Add a little logic for evaluation, and we’re done with the data representation of Digit solutions:

sealed class Expr {

  abstract val value: Int

  data class IntExpr(override val value: Int) : Expr() {
    override fun toString() = value.toString()
  }

  data class BinaryExpr(
    private val left: Expr, 
    private val operator: Operator,
    private val right: Expr
  ): Expr() {

    override val value get() =
      when (operator) {
        Operator.PLUS -> left.value + right.value
        Operator.MINUS -> left.value - right.value
        Operator.TIMES -> left.value * right.value
        Operator.DIVIDED_BY -> {
          check(right.value != 0 && (left.value % right.value != 0))
          left.value / right.value
        }
      }

    override fun toString() = "($left $operator $right)"
  }
}

Solver

If a Digits puzzle can be solved with a particular expression tree, then we can find that solution by constructing every possible expression tree from our set of numbers, and choosing the one which evaluates to the target number. Due to the recursive structure of our expressions, I’m using a recursive, depth first search algorithm as follows:

1. Consider the base case; if the target number is already in our set of numbers, then the solution is simply an integer expression of the target. Easy peasy.
2. Otherwise, create a new subset of numbers to search by applying an operation to a number n, and the target number.
3. Recursively search for a solution with the new target and the remaining numbers. If one exists, return a new binary expression corresponding to the operation and n that we chose.

object Digits {

  fun solve(target: Int, numbers: Set<Int>) = 
    solveInternal(target = target, numbers = numbers)

  private fun solveInternal(target: Int, numbers: Set<Int>): Expr? {
    if (target in numbers) {
      return Expr.IntExpr(target)
    }

    val pairsToSearch =
      Operator
        .values()
        .flatMap { op ->
          val numbersToSearch =
            when (op) {
              Operator.PLUS, 
              Operator.MINUS, 
              Operator.DIVIDED_BY -> numbers
              Operator.TIMES -> numbers.filter { target % it == 0 }.toSet()
            }

          numbersToSearch.map { n ->
            val newTarget =
              when (op) {
                Operator.PLUS -> target - n
                Operator.MINUS -> target + n
                Operator.TIMES -> target / n
                Operator.DIVIDED_BY -> target * n
              }
            Triple(n, op, newTarget)
          }
        }
        .shuffled()

    for ((number, operator, newTarget) in pairsToSearch) {
      val newNumbers = numbers.minus(number)
      val solution = solveInternal(
        target = newTarget, 
        numbers = newNumbers
      )

      if (solution != null) {
        return Expr.BinaryExpr(
          left = solution,
          operator = operator,
          right = Expr.IntExpr(number)
        )
      }
    }

    return null
  }
}

And finally, we solve:

fun main(args: Array<String>) {
  Digits.solve(
    target = 469,
    numbers = setOf(5, 7, 11, 13, 19, 23)
  )
}

Performance

Some implementation details:

• The rules dictate that there are no fractions allowed, so we don’t need to consider a multiplication operation for numbers n that are not fractions of the target.
• While it is not explicit in the rules, I’ve never seen a Digits puzzle with duplicate numbers, so a Set seems like the most performant way to represent the candidate numbers.

For the puzzle that stumped me, Digits.solve(469, setOf(5, 7, 11, 13, 19, 23)) produces an answer in ~43ms, which is 62,000x faster than me. On the other hand, it took 30 minutes to write the algorithm, so the total speed only improved by ~30%. To keep that speedup factor above 1, I will not be attempting any other optimizations.

Thanks for reading! If you have ideas for optimizations and improvements, please play with the code and let me know.